【翻訳】Magic Math – Mulligans By Frank Karsten
2015年11月12日 【翻訳】
省略、意訳、行間の補足等を含みますので、是非原文(http://www.channelfireball.com/articles/magic-math-mulligans/)もご覧ください。
以下翻訳
プロツアー戦乱のゼンディカーのTop8マッチはどの試合もマリガンの決断が試合を分けたと言っても過言ではないものばかりであった。
マリガンはマジックの中でも特に試合結果に密接な概念の一つだが、その本質的な議論は避けられがちで、この手札ならキープ？マリガン？といった程度の意見交換がなされているのが常である。
この記事では、確率論的な立場からマリガンの本質的な側面について考察し、マリガンについて幾らかの判断基準を提供できればと考えている。
まずは先のプロツアー準決勝の第2試合目から例を示そう。
ダブルマリガンの後、瀧村氏は以下の5枚のカードを引いていた。
《始まりの木の管理人/Waden of First Tree》
《棲み家の防御者/Den Protector》
《ドロモカの命令/Dromoka’s Command》
《アブザンの魔除け/Abzan Charm》
《真面目な訪問者、ソリン/Sorin, Solemn Visitor》
瀧村氏はしぶしぶながら3回目のマリガンをし、相手のフラッドも相まって奇跡的に勝利を手にすることができた。
その数時間後、決勝戦の第4戦目で玉田氏がワンマリガンの後に手にしていた6枚が以下の通りである。
《ヴリンの神童、ジェイス/Jace, Vryn’s Prodigy》
《焦熱の衝動/Fiery Impulse》
《道の探究者/Seeker of the Way》
《カマキリの乗り手/Mantis Rider》
《宝船の巡航/Treasure Cruise》
《ゼンディカーの同盟者、ギデオン/Gideon Ally of Zendikar》
玉田氏はこの初手をキープし、1ターン目に土地を引けずそのままゲームを落としてしまった。
両者の下した決断は果たして正しかったのであろうか？
両者の試合結果だけではマリガンの是非を論ずることはできないが、積極的なマリガンが勝敗にどのような影響を与えるかを理解するきっかけにはなったであろう。
以下の2つの例から考察を進めていこう。
例１
あなたは先行で、スタンダードのアブザンアグロを使用している。
7枚のオープンハンドは以下の通りであった。
《乱脈な気孔/Shambling Vent》
《平地/Plains》
《搭載歩行機械/Hangarback Walker》
《先頭に立つもの、アナフェンザ/Anafenza, the Foremost》
《ドロモカの命令/Dromoka’s Command》
《アブザンの命令/Abzan Charm》
《包囲サイ/Siege Rhino》
あなたのデッキにはフェッチランド込みで緑が出るマナソースが18枚ある。
言い換えれば、残りのデッキの1/3が引きたいカードで、残りの2/3が引きたくないカードという訳だ。
Q:最初の2ドローで緑が出る土地を引く確率は次の4つの内どれか？
A. 1/3*1/3=1/9 [11.1%］
B. (1/3*2/3)+(2/3*1/3)＝4/9 [44.4％]
C. 1-(2/3*2/3)=5/9 [55.6％]
D. 1/3+1/3＝2/3 [66.7％]
答え
C.
残りのデッキの中に不要なカードは53-18＝35枚残されていることになる。
したがって正確な答えを書くなら1-(35/53)*(34/52)＝56.8％となるが、試合中に計算機を使うことはできず、頭の中で計算するにしてもスロープレイの警告を受けかねない。
この場合はマリガンの判断の為におおよその確率が分かれば良く、デッキ枚数が減ることを考慮しても、18/53は1/3として扱っても別段問題は無いはずだ。
ではなぜ答えがCになるのであろうか？そのためにまずDが答えではないことを示そう。
Dのロジックを用いると、緑が出る土地を引くために4回ドローしたとすると、目当ての土地を引く確率は1/3+1/3+1/3+1/3となりその総和は1を越えてしまっている。
つまり100％以上の確率が存在してしまうことになるからこれは誤りだ。
読者の中には確率計算に明るくない人もいるだろうから要点だけを述べると、「かつ」は事象の確率をそれぞれ掛け合わせることで「または」はそれぞれの和を取ることを意味する。
つまり排反な2つの事象が起きる確率をXとYとすると、それらが同時に起こる確率はX*Yであり、2つの内どちらかの事象が起きる確率はX+Yとなる。
したがってAの答えは2回のドローで緑が出る土地を2枚引く確率を表しており、Bの答えは2回のドローで緑が出る土地を1枚だけ引く確率を表していることになる。
この両者の確率を足し合わせたのがCだということにお気づきだろうか。
実際にこの通りに求めても良いのだが、2回のドローで緑が出る土地を1枚も引かない確率(2/3*2/3)を求めて全体の1から引いた方が圧倒的に早く計算できるだろう。
今回の場合、どちらの方法で計算したとしてもまずまずの確率で緑のが出る土地を引けることが分かるはずだ。
Q:相手のデッキが分からない場合、この手札をキープすべきか否か
私の結論
キープすべき
ここまでの計算から、3ターン目までに緑が出る土地を引ける確率はおよそ5/9で、引けない確率がおよそ4/9だということが分かっている。
しかしながらそれだけではマリガンをすべきかどうかの判断を下すことはできない。
3つの要素を追加して考えてみよう。
１．
この初手をキープし3ターン目までに緑が出る土地を引けた場合、ゲームに勝てる見込みはあるだろうか？
この問いかけには2回のドローで《森/Forest》と《梢の眺望/Canopy Vista》、もしくは《吹きさらしの荒野/Windsept Heath》と《包囲サイ/Siege Rhino》、もしくは《梢の眺望/Canopy Vista》と《棲み家の防御者/Den Protector》等といった組み合わせを引けるかどうかという点に帰着する。
引いてきた《梢の眺望/Canopy Vista》のタップインが致命傷になったり、そもそも相手の手札が自分より強いことも考えられるが、それでもアブザンアグロというデッキはマナカーブに沿ってしっかり展開できるかどうかをキープ基準とすべきだ。
土地さえ引けばかなり強い手札なので、この初手をキープすれば70％程度の確率でゲームに勝利できるだろう。
２．
3ターン目までに緑が出る土地を引けなかった場合、ゲームに勝てる見込みは果たしてあるのだろうか？
実際には相手が土地事故を起こすことも考えられるため、仮にこちらの土地が詰まってしまっても何とかなることもあるだろう。
仮に3回目のドローまでに緑が出る土地を引けなかったとしても《搭載歩行機械/Hangarback Walker》がなんとか時間を稼いでくれるかもしれない。
しかしながら3回目のドローステップまでに緑が出る土地を引けなかった場合の勝率は残念ながら10％程度しかないだろう。
３
そもそもマリガンをした場合の勝利期待値はどの程度のものなのか？
この問いかけはマリガンをする度に頭をよぎることであろう。
手札が6枚の時の勝利期待値は？5枚なら？4枚だったなら？
Magic Onlineのデータ(http://www.mtggoldfish.com/metagame/breakdown/standard)と私自身の経験則からすると、マリガンを一回した場合の勝率はおよそ40％といったところだろう。
このような問いかけを議論の場で持ち掛けると、数値から導かれる答えではなく、どうしても経験則に頼った答えが返ってくることが多い。
しかしながらトーナメントプレイヤーは調整の段階から様々なシチュエーションを想定しており、理論的にではないにしても確固たる答えを導ける経験値こそが彼らの強みであろう。
上の要素１,２から導かれる勝率は5/9*7/10+4/9*1/10=13/30 [43.3%]程である。
この計算は至ってシンプルなものなので慣れてしまえば一瞬で答えが導かれるだろう。
この43.3％という数字は要素３で導出されたマリガン後の勝率40％よりも大きい値であるため、1回目のマリガンをすることを肯定する根拠足り得るはずだ。
もし初手を眺めてキープするかどうかを迷った時には、ここまでに示した簡単な計算や要素の検討をしてほしい。
そうしたらいつだって2通りの結論に至るはずだ。
一つ目の結論としては、初手に土地は十分揃っていもののそれ以外のカードがぱっとしない場合(除去が全く無い場合など)は、先ほど例として挙げた3ターン目までに緑が出る土地を引ける確率を基準に考えてほしい。
つまり今回の場合なら除去を引ける確率が55.6％未満であるならマリガンだ。
もう一つの結論、は土地を後1枚引けば良い初手を手にしたとき、欲しい色が出るカードがデッキの中に12~13枚(リミテッドなら8枚)しかないのであればそれはマリガンすべきだ。
言い換えるなら、2ターン目までに望み通りの土地を引ける可能性が50％未満であるなら即マリガンである。
例２
モダンのストームデッキで、後手ワンマリガン後に以下のような6枚を引いたとしよう。
《ギタクシア派の調査/Gitaxian Probe》
《手練/Sleight of Hand》
《手練/Sleight of Hand》
《発熱の儀式/Pyretic Ritual》
《紅蓮術士の昇天/Pyromancer Ascension》
《ゴブリンの電術師/Goblin Electromancer》
マリガン後の占術、1ドロー、《ギタクシア派の調査/Gitaxian Probe》があるため、後手1ターン目のドローで土地を引くチャンスが最大で3度ある。
モダンのストームデッキに含まれる土地は18枚程度であることが多く、今回は簡単の為に残りのデッキの1/3が青が出る土地で、2/3がそれ以外のカードだとしよう。
Q:デッキトップ3枚の内、青が出る土地が少なくとも1枚はある確率は？
A. 1/3*1/3*1/3 = 1/27 [3.7%]
B. 3*(1/3*2/3*2/3)=4/9 [44.4%]
C. 1–(2/3*2/3*2/3)=19/27 [70.4%]
D. 1/3+1/3+1/3=1 [100%]
答え
C.
この問題はそれほど複雑な問題ではない。例１から引けるカードが1枚増えただけのことさ。
X枚のデッキの中にY枚の不要牌があるとしたときに、Z回のドローで少なくとも1枚以上の有効牌を引ける確率は1-(Y/X)^Zで表される。
この計算式はDの値が大きくなるほど、すなわち多くのドローを考慮すればするほどデッキ枚数Xのの減少分が誤差として現れる。
正確な値を求めようとすれば超幾何分布計算機(http://stattrek.com/online-calculator/hypergeometric.aspx)のようなものを使わざるを得ないが、大体の値でもキープかマリガンを判断する目安にはなるだろう。
Q:どんなデッキを使っているか分からない相手が初手7枚をキープしたとき、こちらはこの手札をキープすべきか否か。
私の結論
キープすべき
もう一度3つの要素を確認してみよう。
1.
この初手をキープしデッキトップ3枚の中に土地があった場合の勝利期待値は60％ほどだろう。
初手の6枚にはコンボデッキが必要とするキーカードが全てが含まれており、上のアブザンのものと比べてもかなり強い初手だと言える。
しかしながら一度マリガンをしてしまっているのは事実で、2枚目3枚目以降の土地を引けなければやはり苦しい。
以上を鑑みると勝利期待値は上のアブザンの例よりも低い60％程度になると言わざるを得ないだろう。
2.
この初手をキープしデッキトップ3枚の中に土地が無かった場合はどうだろうか。
残念ながらその場合の勝てる見込みは5％ほどである。
土地無しで勝てるほどモダンは甘くないのだ。
3.
再度マリガンして初手5枚で始めた場合の勝利期待値は28％ほどである。
この値は初手6枚で始めた場合のものより小さい値だ。
少し解説を加えると、キープした場合の勝利期待値は１,２の場合を合わせて考えて19/27*60%+8/27*5%=43.7%であると言えるだろう。
この計算を頭の中で行うとなると中々に厄介だが、19/27を少し多く見積もって7/10とし5％をやや少なく見積もって0％とするとすんなり計算できるはずだ。
ここまでの計算結果から、今回の場合は6枚の初手をキープした方が良いことが分かる。
重要なパーツが多いコンボデッキだからこそ、これほどまでにキーカードが揃っているハンドであれば、自分が先手の場合であったり《ギタクシア派の調査/Gitaxian Probe》が無い場合でもキープして良さそうだ。
覚えておくと便利な指標
ここまで挙げてきた例はどれも土地1枚を引ける確率を計算をすれば良い単純なものであった。
しかしながら、実際の試合では目的のカードを2枚もしくはそれ以上引ける確率を計算しなければならないこともあるだろう。
そうなると計算は飛躍的に複雑になり、私自身そのような場に出くわしたことも少なくはない。
そんな時の為に、覚えておけば計算がぐっと楽になる方法をいくつかお教えしよう。
ポーカーの確率計算なんかがここでは良い例だ。
もしあなたがプロのポーカープレイヤーにその局面における勝率を尋ねたとしたら、必ずしっかりとした答えが返ってくることだろう。
当然彼らが複雑な計算を頭の中で瞬時にこなしている訳ではなく、ありふれた局面における確率はあらかじめ把握してしまっているだけの話である。
もしあなたが60枚ではなく52枚のデッキを作らなければならなくなったとしても、必要な土地の枚数はデッキ全体の45％程度であることは経験からも分かることであろう。
それが53枚のデッキであれば必要な土地の枚数は24枚程度であるし、33枚のデッキを作るなら必要な土地の枚数は15枚だ。
このような二項的な計算をする場合には、記事右上1枚目の表を参考にしてほしい(デッキ枚数の多寡には依らないためどんな場合でも使用できる)。
縦はドロー枚数で、横は少なくとも必要な有効牌の数である。
特に覚えておくべきなのは以下の事実であろう。
・デッキの45％を占めるカード(土地)を2回のドローで少なくとも1枚引く確率は70％である。
・デッキの45％を占めるカード(土地)を3回のドローで少なくとも2枚引く確率は43％である。
・デッキの45％を占めるカード(土地)を4回のドローで少なくとも3枚引く確率は24％である。
もう一つ覚えておきたいのがマリガンをしたときの勝利期待値だ。
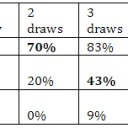
勿論、勝利期待値はフォーマット、自分と相手の使用するデッキ、相手のマリガンの有無などに左右されるが、大体の場合は記事右上2枚目の表が目安になるだろう。
このデータは様々なフォーマットにおけるRolle’s replay scraping bots(http://www.mtggoldfish.com/metagame/breakdown/standard)の昨年一年のデータと私自身の経験に基づいており、昨年までからの大きな変更点となったバンクーバーマリガンの影響を加味して調整を加えたものになっている。
したがって、バンクーバーマリガンの影響を加味した部分は確かなデータに依るものではないが、ある程度合理的な値にはなっているはずだ。
一度マリガンした後の勝率は40％であるため、7枚の初手をキープした時の勝利期待値が40％を越えるのであればそのままゲームを開始するのが賢明であろう。
以上二つの指標を示したわけだが、今度は実際にプロツアーのTOP8マッチに当てはめて考えてみることにする。
先ずは瀧村氏の手札だ。
《始まりの木の管理人/Waden of First Tree》
《棲み家の防御者/Den Protector》
《ドロモカの命令/Dromoka’s Command》
《アブザンの魔除け/Abzan Charm》
《真面目な訪問者、ソリン/Sorin, Solemn Visitor》
Q:後手でこの手札をキープした場合、3ターン目までに土地を3枚引ける確率は？
答え
約14%
草稿ではこの問いの答えを24%としていたが、それは誤りであることが分かった。
占術は実質的にはカードを引くこととは違うため、デッキトップから二枚以上の有効牌を探す場合は、1枚の有効牌を引く場合の確率をそのまま適用することはできなかったのである。
仮にデッキトップが土地ー土地ー呪文ー土地という並びになっていたとして、占術後に3枚引いたところで目当ての3枚の土地を手にすることはできないことが分かるだろう。
正しい確率を求めるためには、まずデッキトップ2枚の内少なくとも1枚が土地である確率を調べ、その後にドローするカードが2枚とも土地である確率との積を取れば良い。
記事右上1枚目の表から見て取れるように、前者の確率は70％で後者は20％であることから、この場合の求めたい確率は両者の積を取って14％となる。
Q:アブザンミラーで相手が6枚の手札をキープした時、こちらはこのハンドをキープすべきか否か？
私の結論
マリガンすべき
3ターン目までに3枚土地を引けた場合の勝利期待値は40％ほどだろう。
低すぎるように思うかもしれないが、相手より手札が一枚少ないことを忘れてはならない。
仮に都合良く土地を引けたとしても、この手札ではミラーの後手を捲るは難しいだろう。
なぜなら《ドロモカの命令/Dromoka’s Command》を有効に使うためにはクリーチャーの線が細く、相手がマナカーブ通りに動いてきた場合には除去が足りないからだ。
ここまでは上手く土地を引ける前提で話を進めていたが、3ターン目までに3舞の土地を引けなかった場合の勝利期待値は5％にも満たないだろう。
4ターン目までに土地を3枚引けた場合の勝利期待値は雑に見積もって15％ほどで、それ以降にもなると目も当てられない確率になるだろう。
ここまでの計算から導かれるこの5枚の手札をキープした時の勝利期待値は14%*40%+86%*5%=10%程度であると言わざるを得ない。
それに対してマリガンをした場合の勝利期待値は記事右上2枚目の表から15％ほどである。
このように勝利期待値を求める際には、経験から来る直観が少なからずの影響を及ぼしていることに留意しなければならない。
勿論この直観は論理性には乏しく、プレイする人が違えば経験してきたことも違う訳であるから、その場合は当然違った勝利期待値の見積もりがなされるはずだ。
しかしながら、ある特定の限られた局面における勝利期待値を求める際には、そういった経験に基づく直観こそが凝り固まった固定概念を打破し得る訳であって、日頃からそういった局面を想定した議論を重ねておけば、いざという時に問題の核心を突く事ができるだろう。
次に玉田氏の手札を見てみよう。
《ヴリンの神童、ジェイス/Jace, Vryn’s Prodigy》
《焦熱の衝動/Fiery Impulse》
《道の探究者/Seeker of the Way》
《カマキリの乗り手/Mantis Rider》
《宝船の巡航/Treasure Cruise》
《ゼンディカーの同盟者、ギデオン/Gideon Ally of Zendikar》
Q:後手でこの手札をキープした場合、2ターン目までに2枚の土地を引ける確率は？
答え
約32％
当初は43％が答えだと思っていたが、瀧村氏のところでも述べた通り占術とドローの違いを考えると正しくは32％となる。
正しい確率を求めるためには、まずデッキトップ2枚の内少なくとも1枚が土地である確率を調べ、その後にドローするカードが土地である確率との積を取れば良い。
記事右上1枚目の表から前者の確率は70％、後者は45％となり、両者の席を取れば正しい確率である32％が得られる。
相手がアブザンで7枚の手札をキープした場合、こちらはこの手札をキープすべきか否か？
私の結論
マリガンすべき
仮にこの初手をキープして順調に2枚の土地を引けた場合の勝利期待値は50％ほどだろう。
なぜなら2ターン目に《ヴリンの神童、ジェイス/Jace, Vryn’s Prodigy》を出すことができれば、ルーター能力で《カマキリの乗り手/Mantis Rider》を出すために必要な土地を探しに行けるからだ。
しかしながら2枚目の土地を引けなった場合の勝利期待値は5％ほどになってしまうだろう。
これらの考察から、この手札をキープした場合の勝利期待値は32%*50%+68%*5%=19.4%ほどであることが分かる。
記事右上2枚目の表を見ると、マリガンした場合の勝利期待値は28％ほどであるため、今回の場合は積極的にマリガンした方が良いだろう。
総括
キープかマリガンの判断は依然として複雑な思考を伴うが、当記事ではその助けとなるいくつかの指標を示せたのではないかと思う。
今後マリガンの判断を誤ってしまうことがあるかもしれないが、単に運が悪かったで終わらせることもマジックを楽しむ上では大切なことだよ。
以上翻訳
語り
コメント